Sign up for the Starts With a Bang newsletter
Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all.
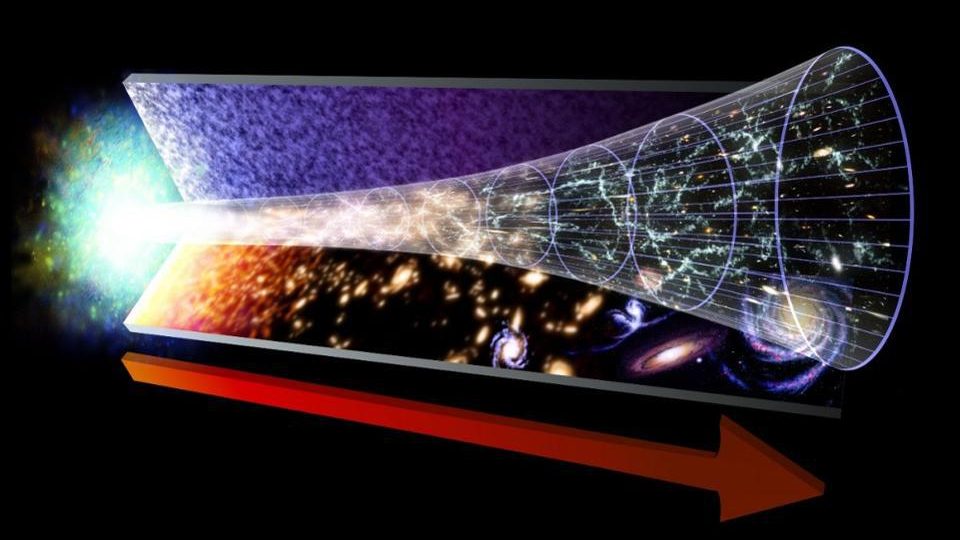
In many ways, our modern picture of the Universe got its start in the 1920s. In that one decade, we discovered that the spiral and elliptical nebulae in the sky were actually galaxies, far beyond the extent of our own Milky Way. We measured the distance to these galaxies, determining that the farther away they were, on average, the faster they appeared to be speeding away from us. And we calculated that a Universe that was uniformly filled with “stuff” — whether matter, radiation, a cosmological constant, or any other form of energy — would be unable to be static and stable; it must either expand or contract.
From these revolutionary realizations, the notion of the expanding Universe was born. Over the past century, we’ve learned much more about the history and properties of our Universe. We know it’s been 13.8 billion years since the hot Big Bang; we know our Universe is dominated by dark energy and dark matter; we know that the hot Big Bang was preceded and set up by a period of cosmic inflation. But what came before inflation, and could the inflationary period have lasted forever? That’s what David Aiken wants to know, writing in to ask:
“What are the implications of the Borde Guth Vilenkin theorem? If the universe is now and has always been spatially infinite, the why couldn’t it be expanding on average for ever? Or, given inflation, have no actual beginning but just approaches some limit ab infinitum?”
It’s a wonderfully deep question, and one that everyone who’s curious should learn the answer to. Here’s what the Borde-Guth-Vilenkin (or BGV) theorem is all about, plus what it means (and what it might mean) for our Universe.
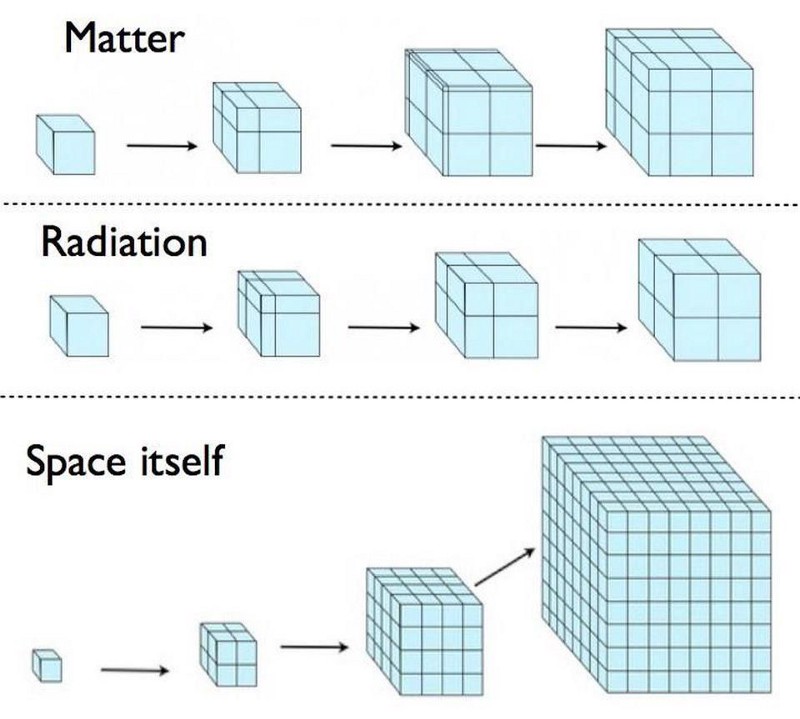
How matter (top), radiation (middle), and dark energy/inflationary energy (bottom) all evolve with time in an expanding Universe. As the Universe expands, the matter density dilutes, but the radiation also becomes cooler as its wavelengths get stretched to longer, less energetic states. Dark energy’s (or inflationary energy’s) density, on the other hand, will truly remain constant if it behaves as is currently thought: as a form of energy intrinsic to space itself. These three components, together, dictate how the Universe expands at all times from the Big Bang until the present day and beyond.
What you see, above, is an illustration of how the density of the Universe changes based on what’s in it as it expands. For normal matter, which we generally consider as being made of massive particles that are moving slowly compared to the speed of light, the density is just the mass of each particle multiplied by the number of particles divided by the volume that the particles occupy. As the Universe expands, the volume increases, while the particle masses and the total number of particles remains the same. Therefore, in an expanding Universe dominated by matter, the density drops with time, and so does the expansion rate.
For radiation, the quanta are massless (or possess kinetic energies that far exceed their rest mass energy), so its energy density is the energy of each particle multiplied by the number of particles and divided by the volume that they occupy. As the Universe expands, the number of particles remains constant and the volume increases, but the energy of each particle changes as the wavelength stretches: decreasing even faster than the matter density does.
But for dark energy — or inflationary energy, for that matter — its defining feature is that its energy density is the thing that remains constant. As the Universe expands, the expansion rate and energy density both do not change, leading to a relentless state where the Universe doubles in size, again and again, each time a certain interval elapses.
This diagram shows, to scale, how spacetime evolves/expands in equal time increments if your Universe is dominated by matter, radiation, or the energy inherent to space itself (i.e., during inflation or dark energy dominance). The bottom-most scenario corresponds to exponential expansion via both dark energy (today) and inflation (at early times). Note that visualizing the expansion as either ‘the existing space stretching’ or ‘the creation of new space’ won’t suffice in all instances.
This has an interesting set of implications for our expanding Universe, particularly if we start from where we are today and extrapolate backwards in time. You see, even though our expansion rate today is dominated by dark energy, this hasn’t been true for all time. It was only a few billion years ago that dark energy became the dominant factor in our Universe’s expansion; before that, it was the combination of dark matter and normal matter. And even earlier than that, for the first few thousand years after the start of the hot Big Bang, our Universe wasn’t dominated by matter of any type, but by radiation: a mix of photons and neutrinos.
This is because our Universe doesn’t just have one type of energy in it, but many. In truth, our Universe contains a wide mix of ingredients. While today, those contributions are:
- 68% dark energy,
- 27% dark matter,
- 4.9% normal matter,
- 0.1% neutrinos,
- and about 0.01% photons,
the ratios evolve with time. As the Universe continues to expand, dark energy’s relative contributions to the energy density will rise, while the remaining components will continue to decrease in relative importance. Similarly, if we extrapolate back to earlier times, we’ll see the matter components increase in relative importance, but the radiation components increase in importance by an even greater amount.
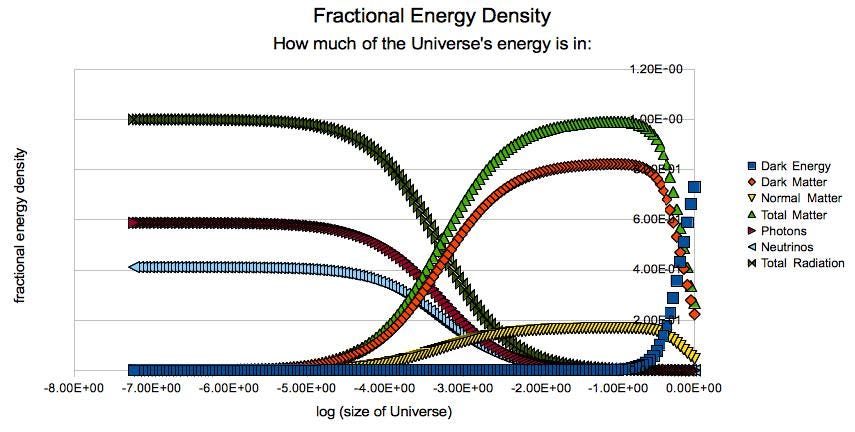
The relative importance of different energy components in the Universe at various times in the past.
Dark matter has been largely important for extremely long cosmic times, and we can see its signatures in even the Universe’s earliest signals. Meanwhile, radiation was dominant for the first ~10,000 years of the Universe after the Big Bang. Note that in the future, when dark energy reaches a number near 100%, the energy density of the Universe (and, therefore, the expansion rate) will remain constant arbitrarily far ahead in time.
For these reasons, we had long assumed that in the early Universe, it would be radiation that was the dominant form of energy that was present. If you extrapolate back and back, to earlier and earlier times, you’d predict that:
- densities would have been greater (because the volume of the Universe was smaller),
- the energy of each quantum of radiation would have been greater (because its wavelength was smaller),
- and that the expansion rate would have been greater (because the expansion rate is proportional to the square root of the total energy density at any given time).
This is why, for most of the 20th century — until the 1980s — people assumed that the hot Big Bang implied a singularity at the beginning. Take a hot, dense state, extrapolate it back to still earlier times, and it just gets hotter and denser, hotter and denser, etc., until the laws of physics break down and you’re left with nothing more than a point of infinite temperature and density.
But starting in the 1980s, we began to consider an alternative scenario: one that’s since been validated by the full suite of cosmic data. Instead of rising up to arbitrarily high temperatures, there was a cutoff: a hottest part to the hot Big Bang. Prior to that moment, there was an inflationary epoch: where the Universe was dominated by a form of energy inherent to the fabric of space itself. And if you compare how a Universe dominated by radiation, matter, or inflationary energy behaves, you’ll find something perhaps unexpected: in the inflationary case, there is no singularity.
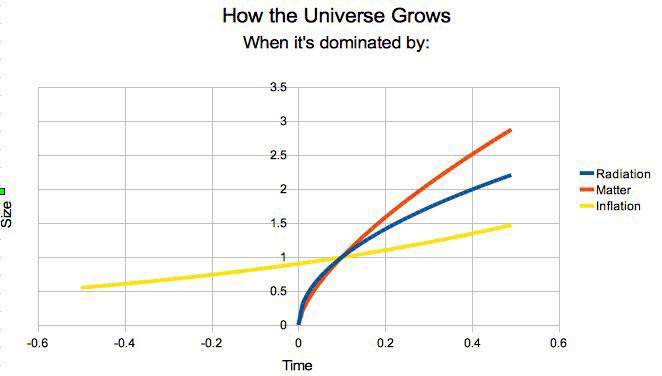
Blue and red lines represent a “traditional” Big Bang scenario, where everything starts at time t=0, including spacetime itself. But in an inflationary scenario (yellow), we never reach a singularity, where space goes to a singular state; instead, it can only get arbitrarily small in the past, while time continues to go backward forever. Only the last minuscule fraction of a second, from the end of inflation, imprints itself on our observable Universe today. The size of the now-observable Universe could’ve been no smaller than about 1 cubic meter in volume at the start of the hot Big Bang.
While the idea of cosmic inflation was profound for many reasons, particularly for the novel implications the idea made that differed from the standard predictions of the arbitrarily hot-and-dense initial state previously implied by the hot Big Bang, what you see above is perhaps its most profound consequence. For decades, the scientific idea of the Big Bang had been viewed as a “moment of creation,” the “starting gun” of our cosmic existence, or as some of the theory’s pioneers called it, a “day without a yesterday,” a “cosmic egg,” or “the primeval atom.” But with inflation replacing the earliest moments of that stage, all of a sudden the story of our ultimate origins was thrown into doubt.
You see, in an expanding Universe dominated by matter or radiation, extrapolating backwards always leads to a singularity: a set of conditions marked by reaching infinite densities and infinite temperatures/energies after a finite amount of time. But in an inflationary Universe, you can only asymptotically approach a state of zero size, which is what you need to obtain infinite densities or temperatures or energies. In fact, it’s easily provable that the inflationary state, which leads to exponential expansion, cannot reach a state of zero size even if you extrapolate back by an arbitrarily large amount of time.
It’s a fascinating property, and it was by investigating these properties of inflationary spacetimes that physicists and mathematicians Arvind Borde, Alan Guth, and Alex Vilenkin came upon what’s now known as the Borde-Guth-Vilenkin (or BGV) theorem.
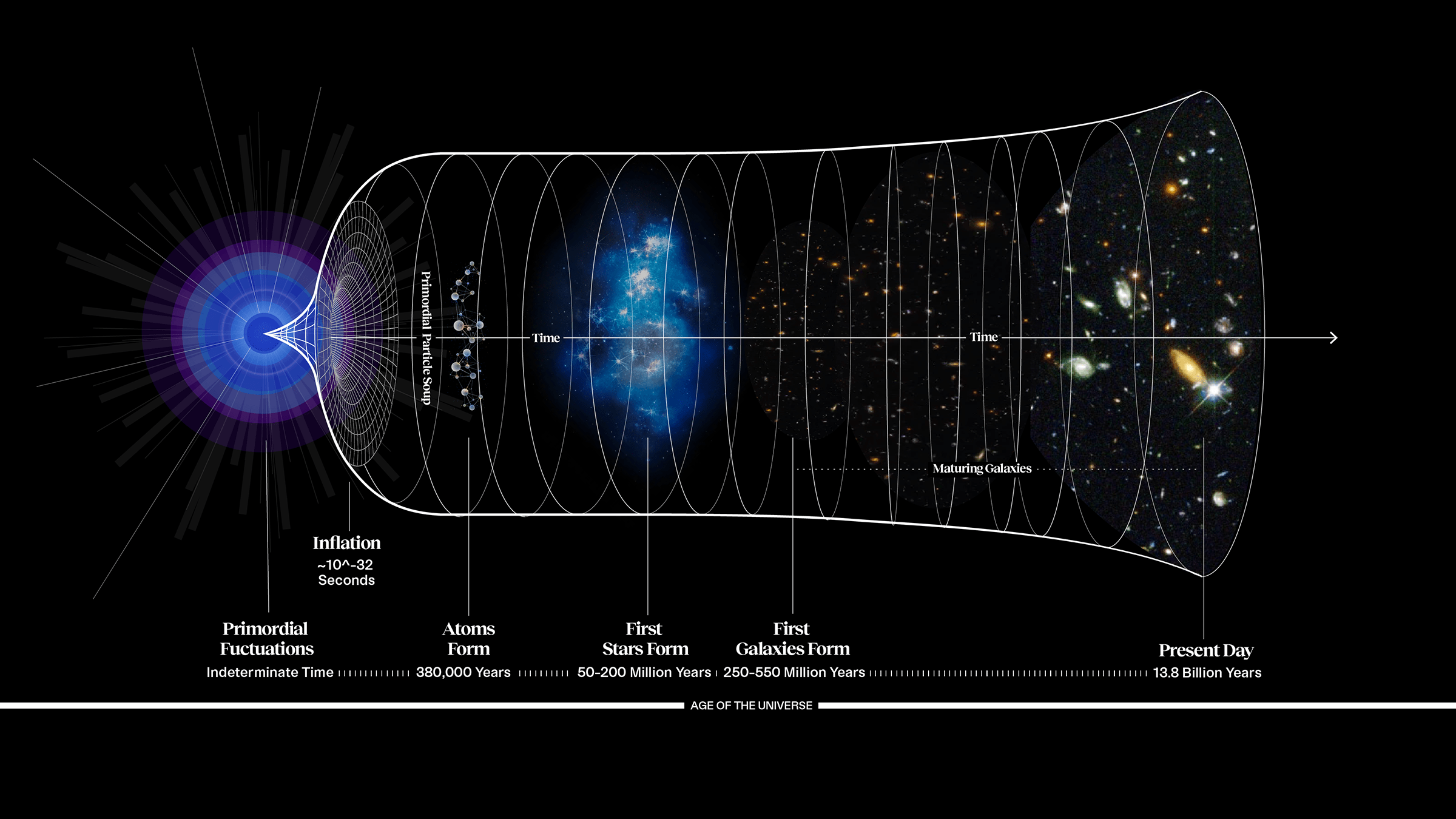
This timeline of the Universe shows how, from a Planck-scale region of space that possessed an inflationary state, the properties of the hot Big Bang were set up beforehand. Once the Big Bang occurs, our Universe becomes filled with a primordial particle soup, which evolves into the atoms, stars, galaxies, and large-scale structure we’re familiar with today. However, unanswered questions about inflation, including what the pre-inflationary state was and how it began, still remain.
The major realization, or proof, that came out of their original paper is often framed in this way: the fact that inflationary spacetimes are past-timelike-incomplete.
On the surface, this might just seem tautalogical. A spacetime that is complete will terminate in an event that “completes” the spacetime: a singularity or a null surface.
- A radiation-dominated expanding Universe will, if you extrapolate it backwards, terminate in a singularity: it’s past-timelike-complete.
- A matter-dominated expanding Universe will, if you extrapolate it backwards, terminate in a singularity as well: it, too, is past-timelike-complete.
- But an inflationary Universe, if you expand that one back in time, will never terminate in a singularity. It isn’t past-timelike-complete, and therefore, it’s past-timelike-incomplete.
“So what,” you might say. “So it’s not past-timelike-complete. Doesn’t that just mean this spacetime doesn’t end in a singularity, and so therefore, couldn’t it have been inflating forever?” And it’s a very reasonable thought: couldn’t a spacetime like this just be inflating forever, eternally, to the past?
The answer turns out to be “no,” and there’s an interesting exercise you can consider to see why.
What you see, above, is a famous example from physics of a ball (or coin, or any “rolling” object) that circles a depression, drain, or other “sink” within Earth’s gravitational field. It’s often used as an analogy for gravitation, where you can imagine that if there were no dissipative forces at play — no friction, no air resistance, and no loss of energy as the rolling object moves around across the surface — that the object would continue in the same orbit forever and ever: similar to how a planet orbits the Sun. It’s a clever demonstration and an excellent analogy, with only slight, minor flaws that require correction at more advanced levels of understanding.
In the demonstration, however, there are dissipative forces, and so the rolling object really will fall deeper and deeper into this potential well. As it moves closer towards the center of the depression, its speed starts to increase, similar to how the inner planets orbit at more rapid speeds than the outer planets in a gravitational system. The deeper and deeper it goes, the faster and faster it goes, with no apparent limit in this type of system you so often see in science museums. Eventually, the rolling object fall all the way into the depression, until it falls completely through the hole at the bottom.

This illustration of inflation shows a series of world-lines, shown three-dimensionally, that all diverge from one another following exponential curves. These world-lines can never cross or meet, but only expand exponentially away from one another as time goes on. Going back in time, they converge, but also never cross or meet, despite the limitations of the resolution of modern screens.
Credit: Ben Gibson / Big Think / Adobe Stock
In an inflationary spacetime, as shown above, you can imagine putting a test particle — a ball, a mote of dust, or just a mathematical point — down anywhere you want in space. You can also imagine putting two test particles down: separated by a very small distance, where maybe one has a tiny speed relative to the other.
If you run the clock forwards, because this is an inflating spacetime, you already know what’s going to happen: the space between those two particles will expand, relentlessly and exponentially. The particles will separate from one another: at a specific rate, initially, or at a certain number (to put it in cosmological terms) of km/s, dependent on the distance between them. As the distance between them increases, they’ll separate at faster and faster speeds, as we typically write the expansion rate of the Universe in terms of a speed-per-unit-distance: in km/s/Mpc.
But what if you ran the clock backwards?
You’d see the two particles get closer and closer, with the speed at which they get closer decreasing, slower and slower, the closer they got. However, if one of those particles was in relative motion to the other, they wouldn’t simply asymptote towards one another like they would if they were static.

This animation shows a ball rolling down into the central hole in a gravitational funnel. As the ball gets closer to the funnel’s center, its speed increases. If the funnel were narrow and thin enough, this would lead to a situation where the ball, confined to narrower and narrower spaces but still compelled to conserve angular momentum, would have to exceed the speed of light, resulting in a pathology. In General Relativity, the pathology would lead to what’s known as a curvature singularity.
Instead, it would behave in an analogous way to the rolling object that was on the curved surface with the hole/depression in the middle of our earlier gravity demonstration. The moving object would “spiral in” and around the other test particle, and would do so at a faster and faster rate the farther back in time we ran the clock.
“Big deal,” you might think, “as we go farther and farther back in time, the particle can just orbit that location faster and faster at smaller and smaller distances, and what could possibly be the problem with that?”
The problem is that you can’t just arbitrarily have something move around faster and faster, like we could (to the limits of our demonstration) in the gravitational-analogue demonstration. This time, we run into a fundamental limit: the fact that particles can’t move through space at a faster speed than the speed of light. As we ran the “clock” of the inflationary spacetime back farther and farther, the speed would continue to increase. At some point, you wouldn’t reach or exceed the speed of light (because that’s impossible), but would encounter a different pathology: a curvature singularity. The inevitability of running into such a problematic situation is just one example of how the inflationary state, in general, is problematic for being past-timelike-incomplete; we’d need a different state to “complete” the spacetime.
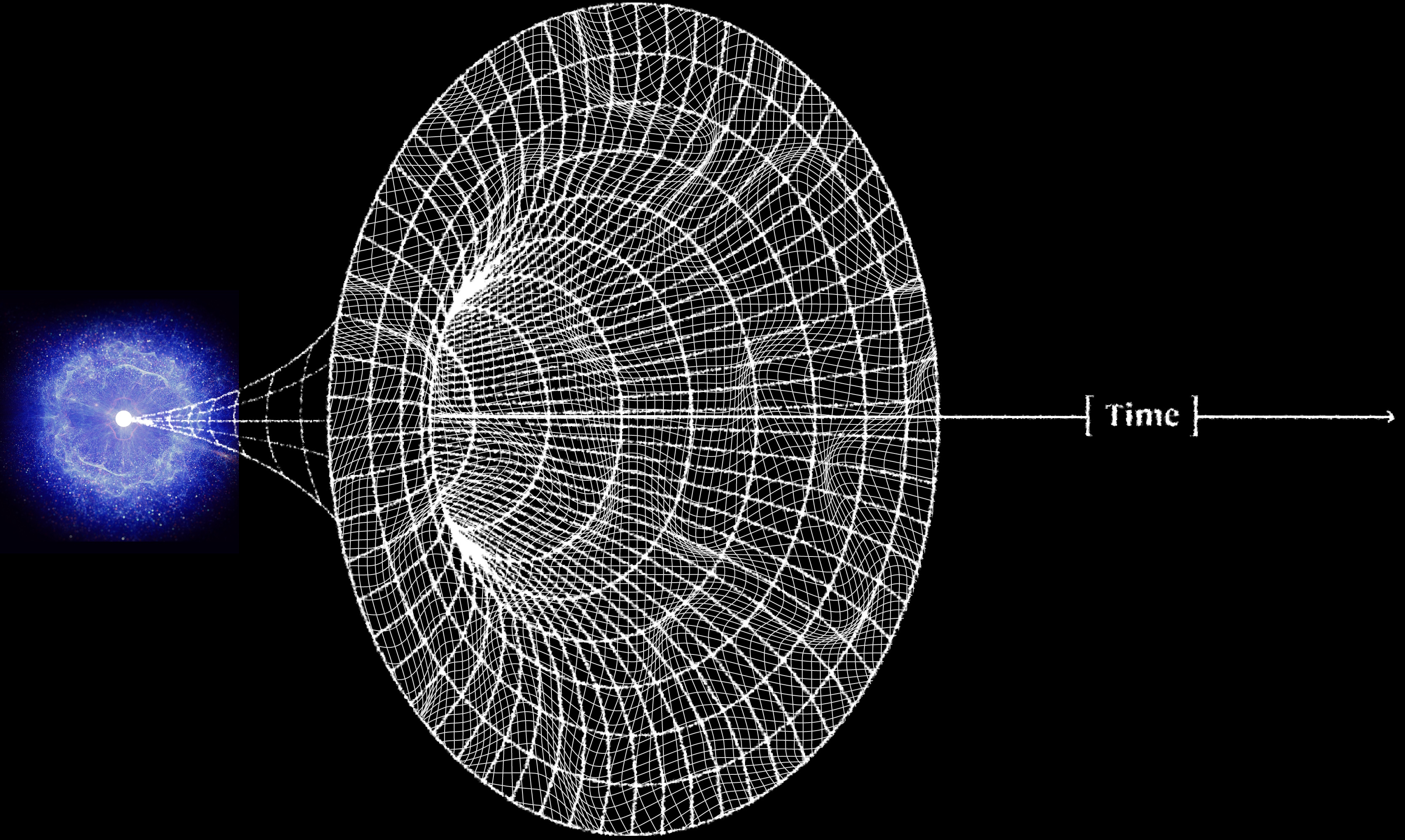
From a region of space as small as can be imagined (all the way down to the Planck scale), cosmological inflation causes space to expand exponentially: relentlessly doubling and doubling again with each tiny fraction-of-a-second that elapses. Although this empties the Universe and stretches it flat, it also contains quantum fluctuations superimposed atop it: fluctuations that will later provide the seeds for cosmic structure within our own Universe. What happened before the final ~10^-32 seconds of inflation, including the question of whether inflation arose from a singular state before it, not only isn’t known, but may be fundamentally unknowable.
And so that’s the big takeaway here: not necessarily that there must be a singularity somewhere along the line, but only that the inflationary state — whatever it is — could not have continued eternally into the past. Some other spacetime state, one that is past-timelike-complete, is what we require. There are all sorts of options here, including:
- a pre-inflationary state that triggered inflation in at least one region, but where that pre-inflationary state itself did begin from a singularity,
- a cyclic or bouncing cosmology that led to the inflationary state, however recent work suggests that those all terminate in an initial singularity in the past direction as well,
- or, and this is one of my favorite scenarios, an inflationary state that asymptotes, in the past, to a constant, static, non-expanding state: one that’s past-timelike-complete, but with no initial singularity at all.
There are plenty of people who still argue over the BGV theorem. Cosmologists and mathematical physicists often seek ways to circumvent the theorem, looking to quantum gravity (or other non-standard scenarios) to break us out of the requirements that General Relativity imposes. Theoretical physicists seek creative ways out: ways to trigger inflation from a variety of potential pre-inflationary states, leveraging important developments like the Bunch-Davies vacuum. And there are people with theological and philosophical bents who use the BGV theorem to bolster their preferred arguments over how the Universe ultimately began, with dubious and debatable results.
But the takeaway point is that even if inflation, once it begins, is necessarily eternal into the future, it could not have been eternal to the past. Some other state, possibly culminating in a singularity but definitely not an inflationary state itself, must have preceded it. With our observable Universe only providing a window into the final tiny fraction-of-a-second of inflation, it may be a long, long time, if ever, before we resolve what that pre-inflationary state actually was!
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Sign up for the Starts With a Bang newsletter
Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all.
First Appeared on
Source link