Neutrinos are still the most mysterious particle we know of

Here in the 21st century, there’s a lot that we’ve uncovered about our Universe that, a mere century ago, would have been mind boggling. Sure, we already knew about general relativity, the existence of subatomic particles, knowledge of radioactivity, and the beginnings of quantum mechanics. But we had yet to discover the expanding Universe and reveal the Big Bang, to recognize that the fields as well as the particles composing the Universe are quantum in nature, or to learn that protons are composed of still smaller, more fundamental entities: the quarks and gluons. The big puzzles of today, including dark matter, dark energy, and the origin of the matter-antimatter asymmetry, could hardly have been fathomed at the time.

But as we continued to investigate the nature of reality through many different avenues:

• through laboratory experiments with radioactive materials,
• through cosmic ray experiments done first with hot air balloons and later, from space itself,
• through underground, well-shielded experiments surrounded with exquisite detectors,
• through high-energy particle physics experiments done with colliders,
• and through a wide array of astrophysical observatories,

we began to piece together a more accurate picture of reality. The zoo of standard model particles and the four fundamental forces, plus the discoveries of dark matter and dark energy, all came into focus in the late 20th century, with many more details uncovered through the first quarter of the 21st. Through it all, however, the humble neutrino remains the most mysterious of all the known particles, and the only known particle with a chance to solve the three biggest mysteries in all the Universe. Here’s how.

Neutrinos got their start way back in 1930, as a purely theoretical proposal to explain a phenomenon that had long been observed: the radioactive decay of atomic nuclei that changed their species of atom by one element by emitting an electron. When these radioactive decays — collectively known as beta decays — occurred, laboratory scientists worked exceedingly hard to measure two main things:

• the masses and kinetic energies of the “daughter” particles (post-decay),
• and the momenta of the “daughter” particles, including both magnitude and direction.

For all other types of radioactive decays, including gamma decays and alpha decays, the total final energy (rest mass energy plus kinetic energy) was conserved, meaning it was equal to the total initial energy. Similarly, momentum was conserved as well: if you added up the magnitude and direction of all the particles involved in the final decay, they added up to the momentum of the initial, pre-decay particle.

But for beta decays, it looked like something was lost. The post-decay energy was always less than the pre-decay energy, and it looked like there was a net amount of momentum that was spontaneously created in the decay process. While some (including even Niels Bohr) favored considering that energy and/or momentum might not be conserved, Wolfgang Pauli had a wild idea to save both energy and momentum conservation: the hypothesis of a new particle. It would be electrically neutral, it would be very very light (or even massless), and it would be very difficult to detect. He named it neutrino: Italian for “little neutral thing.”

Reactor nuclear experimental RA-6 (Republica Argentina 6), en marcha, showing the characteristic Cherenkov radiation from the faster-than-light-in-water particles emitted. The neutrinos (or more accurately, antineutrinos) first hypothesized by Pauli in 1930 were detected from a similar nuclear reactor in 1956.

Initially Pauli lamented his theoretical device, noting that he had proposed a particle that he could not devise a method to detect; its cross-section would be so small that it would take roughly a light-year’s worth of solid lead to result in even a 50/50 shot at causing an interaction. However, Pauli failed to anticipate two major advances that would come in the subsequent years and decades.

• First, we developed an understanding of nuclear physics reactions, and became capable of not just triggering nuclear fission reactions, but of controlling them, leading to nuclear power plants.
• And second, we began to understand how the Sun worked as well, and recognized that it was powered by a different flavor of nuclear reactions — nuclear fusion — that served as the source of its power.

If Pauli’s theory of neutrinos were correct, then each of these sets of reactions, both fission and fusion, would emit neutrinos each with a substantial amount of energy (in the ~MeV, or mega-electron-volt, range) to them. The fission reactions would emit antineutrinos; the fusion reactions would emit regular neutrinos. The key to detecting them, then, wasn’t to simply build a detector sensitive enough to see each individual neutrino; that would be a practically impossible task. However, if you could build a sufficiently large detector that would encounter enormous numbers of neutrinos (or antineutrinos), then eventually, you can start to see the neutrino signature in your detector.

The neutrino was first proposed in 1930, but was not detected until 1956, from nuclear reactors. In the years and decades since, we’ve detected neutrinos from the Sun, from cosmic rays, and even from supernovae. Here, we see the construction of the tank used in the solar neutrino experiment in the Homestake gold mine from the 1960s. This technique, of building neutrino observatories deep underground, has been a hallmark of particle physics experiments for over 60 years.

That was the plan that first led to success in 1956, when a large, fluid-filled detector — one surrounded with detectors that were sensitive to particle signatures generated inside — was placed next to a nuclear reactor that was suspected to be emitting large quantities of antineutrinos while active. Those detections were consistent with the properties of neutrinos: and specifically, of electron antineutrinos that the reactor should be generating.

Similarly, the Sun’s nuclear reactions should be producing regular electron neutrinos, with the energy of those neutrinos falling into an easily calculable range. So if we could build a large detector that was sensitive to neutrinos, then simply running that detector for long enough would result in the detection of those neutrinos.

So we did. We built neutrino detectors deep underground, where they’d be shielded from cosmic rays. We began lining the outside of the detectors with further shielding materials to prevent contamination from radioactive decays and cosmic particles. We refined calculations of the interior of the Sun based on the latest, most up-to-date solar models that we had. We built detectors larger and larger, with photomultiplier tubes surrounding the interior walls and applied electric fields allowing us to detect any stray, ionized particles. And yes, we began detecting these solar neutrinos in great numbers. You’d think that the endeavor was a total success.

Neutrino and antineutrino detectors operate by having a large “target” for neutrinos/antineutrinos to interact with inside of a tank surrounded by photomultiplier tubes, which allow scientists to reconstruct the event characteristics that happened at the source. Sometimes, large external electric fields are applied as well, allowing scientists to construct a second signal based on internal ionization that occurs within the detector from neutrino events.

But we weren’t seeing the right number of neutrinos. More specifically, when we compared our numbers for:

• the expected number of neutrinos generated by the Sun,
• the calculated flux of neutrinos that should be reaching our neutrino detectors here on Earth,
• and the interaction cross-section of neutrinos with the (normal) matter inside those tanks,

they weren’t matching the number of neutrinos our detectors were actually picking up. We were seeing fewer neutrinos — only about ⅓ of the predicted number — that we were anticipating seeing. Even as models were refined, calculations were checked, detectors were calibrated, and independent neutrino detectors were built (but seeing the same result), the discrepancy remained. The problem even got its own name: the “solar neutrino deficit” problem.

This was very unexpected, and led to a lot of different lines of thought. Some thought that the solar neutrino problem was evidence that we didn’t understand nuclear physics in stars well enough at all, and placed the blame there. Others blamed the experimental setup for detecting neutrinos, although it was difficult to figure out what, if anything, was being done wrong. But there was another possibility, one that seemed extremely wild to many. Perhaps these neutrinos weren’t massless, as originally thought. Perhaps they did have masses, even if they were tiny compared to the other known particles. And if they did have mass, then because they were quantum particles with the same quantum numbers as one another (except for lepton family number), then they could mix together, just like quarks of the same quantum number (except for baryon family number) were observed to mix together.

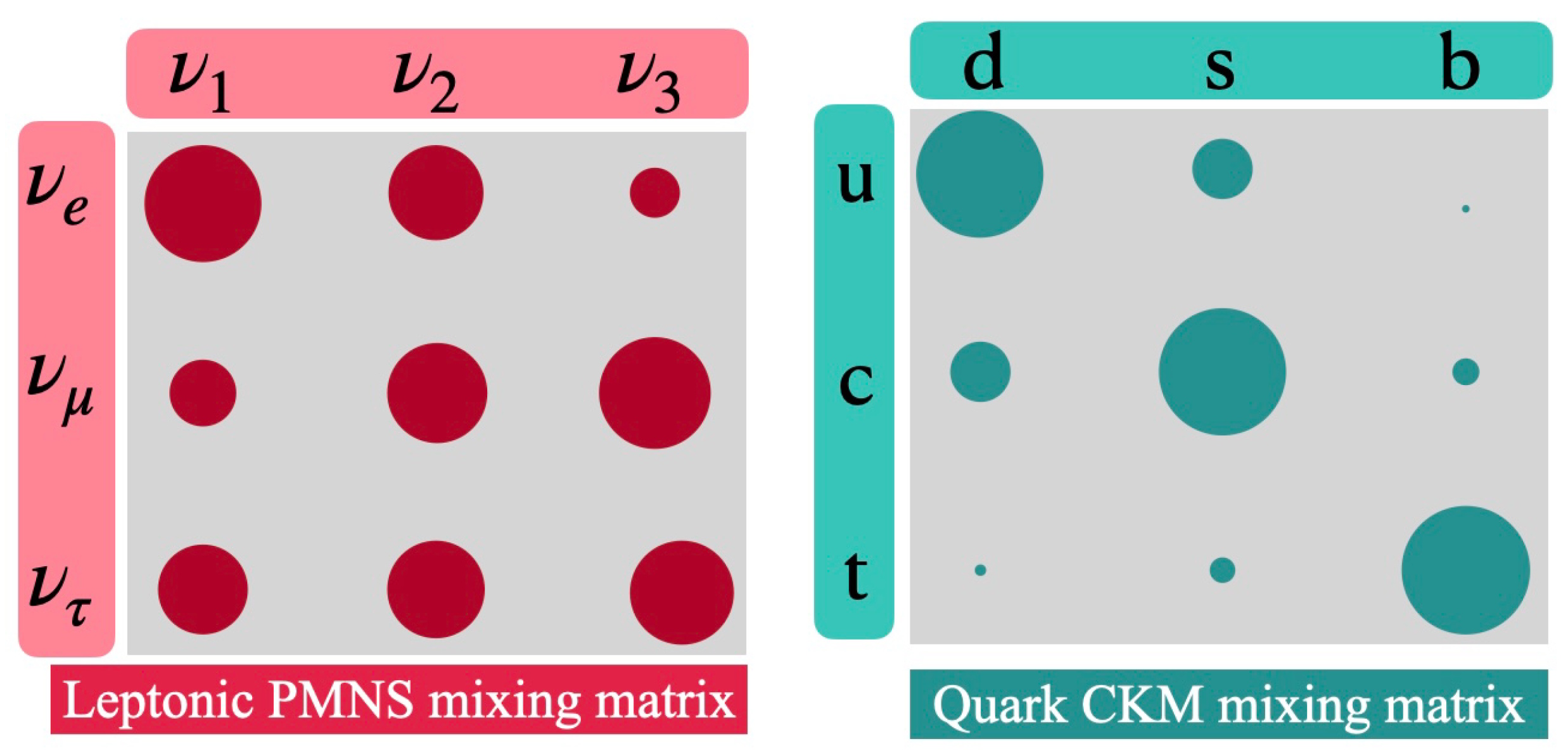
This illustration shows the mixing matrices for neutrinos (left) and quarks (right), which is only possible if the neutrinos and quarks have non-zero rest masses. The fact that there are non-diagonal elements in the neutrino mixing matrix indicates that electron, mu, and tau neutrinos don’t have fixed masses, but instead are superpositions of the three possible mass (1, 2, 3) eigenstates.

If this were the case, then you wouldn’t just have three types of massless left-handed neutrino:

• an electron neutrino,
• a muon neutrino,
• and a tau neutrino,

as well as their three massless right-handed antineutrino counterparts. Instead, what you’d have are three different masses that each neutrino could take on:

• a neutrino with a mass eigenstate (a state that you can observe) of ν₁,
• a neutrino with a mass eigenstate of ν₂,
• and a neutrino with a mass eigenstate of ν₃,

where each of the electron, muon, and tau neutrinos were superpositions of all three mass eigenstates together, but with different probabilities from one another. When a neutrino encounters another particle, it can only interact as an electron, muon, or tau neutrino, but when you measure its energy/momentum, it always corresponds to having a mass eigenstate of ν₁, ν₂, or ν₃. (These would be the same for antineutrinos as well.)

If neutrinos were massive, they’d be incredibly weird. The photon and the gluons of the Standard Model are massless, whereas the massive Standard Model particles range from the electron, at about half-an-MeV, to the top quark, at 173 GeV. But if neutrinos had mass, their masses had to be incredibly low: of less than even one electron-volt, or around a million times lighter than the next-least-massive sets of particles. Still, the proof would come experimentally and observationally, not theoretically. With neutrino detectors that were sensitive to both solar and atmospheric neutrinos, where the latter are generated by cosmic ray showers, we were able to determine that neutrinos are massive, and do indeed oscillate from one flavor into one another.

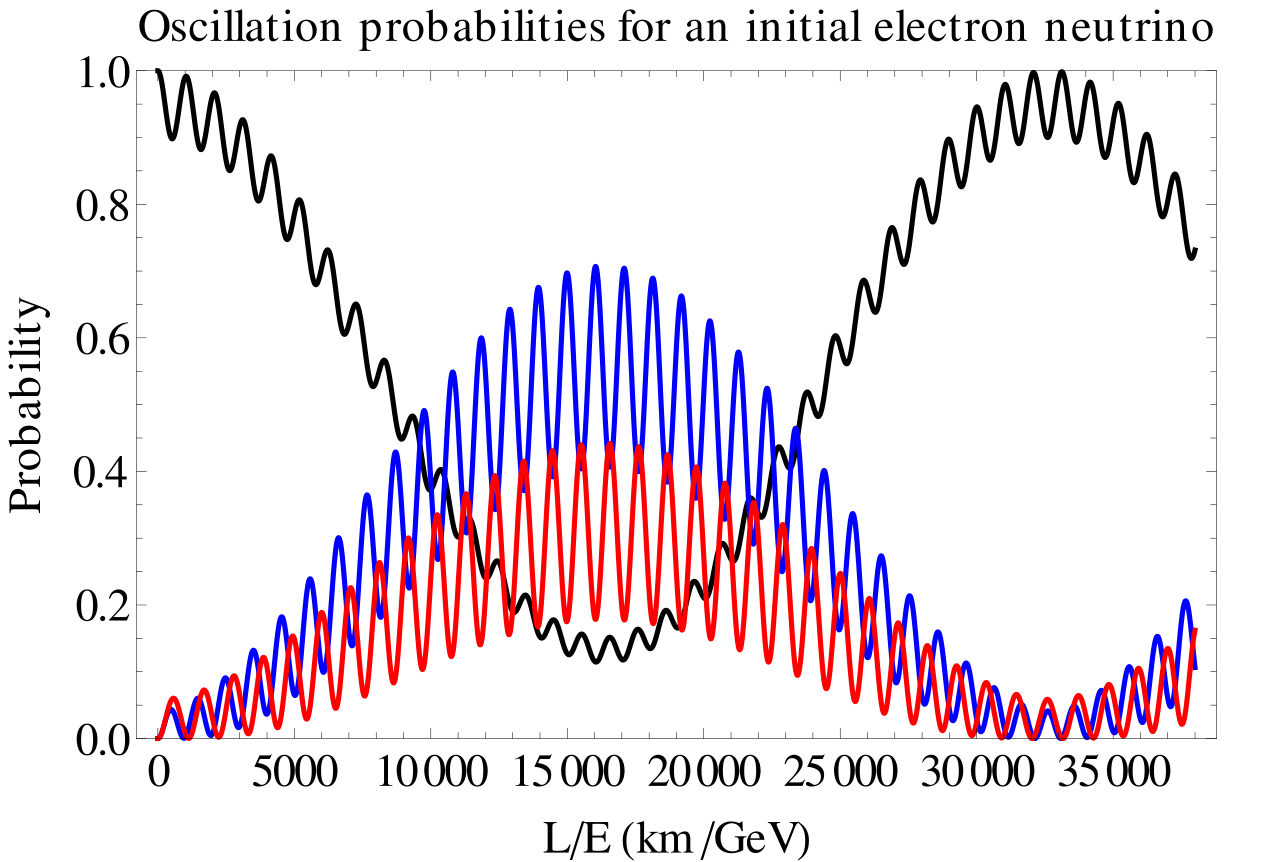
Vacuum oscillation probabilities for electron (black), muon (blue), and tau (red) neutrinos for a chosen set of mixing parameters, beginning from an initially produced electron neutrino. An accurate measurement of the mixing probabilities over different length baselines can help us understand the physics behind neutrino oscillations and could reveal the existence of any other types of particles that couple to the three known species of neutrino. For neutrinos to oscillate, they must have non-zero mass. If additional particles (such as dark matter particles) carry energy away, the overall neutrino flux will show a deficit.

Among other revelations, this solved the solar neutrino problem. The reason we were seeing a deficit of solar neutrinos isn’t because they weren’t there, but rather because they oscillated from being 100% of the “electron type” when they were created into a mix of electron, muon, and tau type neutrinos.

We began performing neutrino experiments with neutrino beams — where you shoot high-energy particles at fixed targets and then send the outgoing debris through the Earth, where everything except neutrinos gets absorbed — where the neutrinos travel through a variety of distances before reaching the detector. This enables us to measure how neutrinos oscillate, and how those oscillations depend on both distance and whether the neutrinos pass through matter or not.

And we began honing in on the rarest decays of the tritium atom: where a nucleus made of one proton and two neutrons beta decays into a nucleus with two protons and one neutron, plus an electron and one (invisible) antineutrino. Where the nucleus and electron have the greatest amounts of kinetic energy, the smallest energy is left over for the neutrino. While we have yet to find the three “steps” that denote the ν₁, ν₂, and ν₃ masses (in whatever order they happen to exist in), we’ve constrained the neutrino masses more tightly than ever.

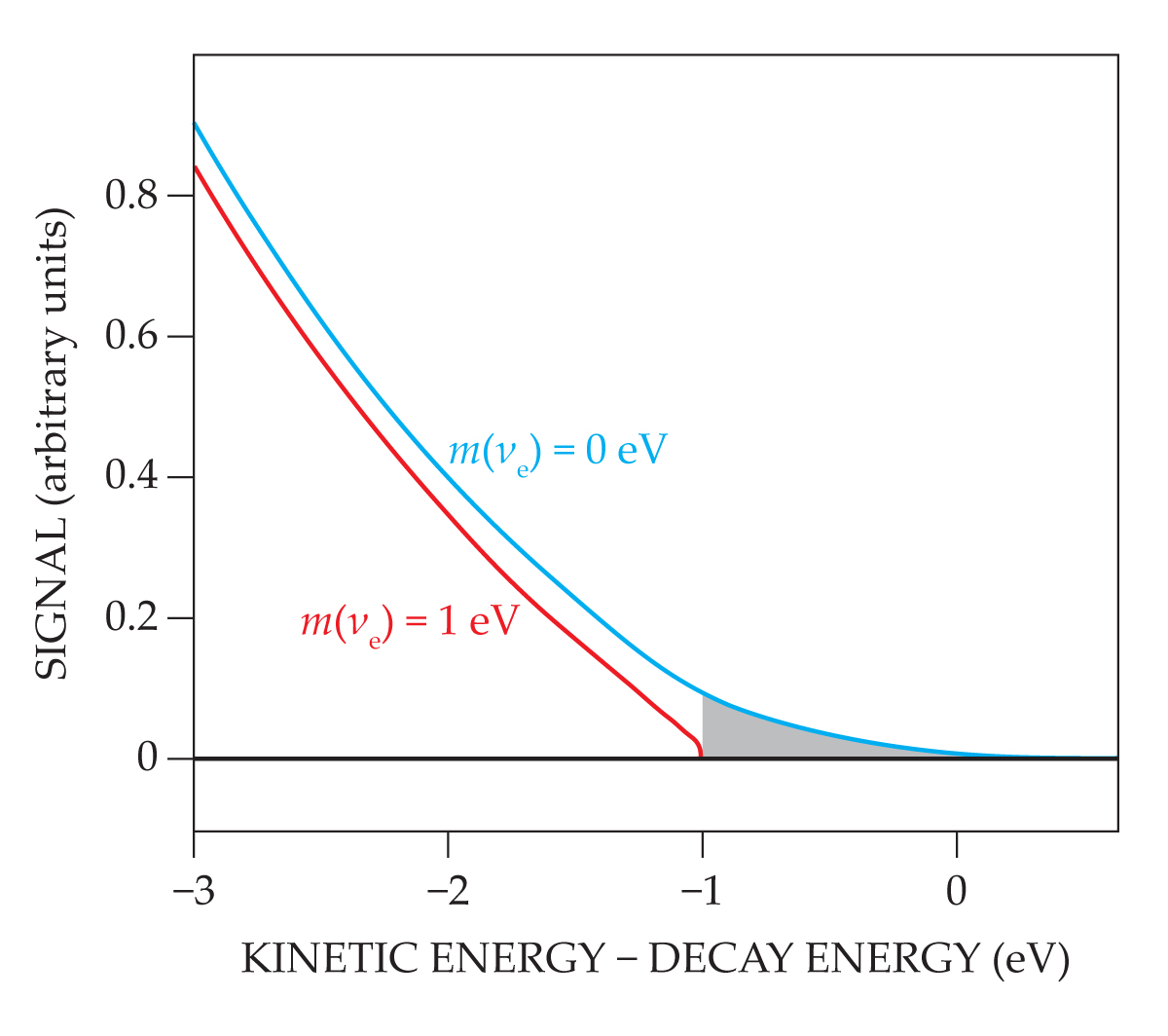
If neutrinos have no mass at all, then the combined mass-and-kinetic energy of the daughter nucleus and electron products resulting from the decay of tritium would follow the blue curve. If instead they follow a curve like the red one, it would provide us with a way to directly measure neutrino mass. This is the technique leveraged by the KATRIN experiment to try to directly measure neutrino masses, with a strong null result thus far.

But this is not the end of the story; this is just where we’ve gotten to so far. There’s so much that we still don’t know about the neutrino. For example:

• in the Standard Model, all neutrinos are left-handed (which means they interact like left-chiral particles),
• while all antineutrinos are right-handed (meaning they interact like right-chiral particles).

At present, all of the fermions of the Standard Model are thought to be Dirac fermions: particles that are distinct and different from their antimatter counterparts. However, if neutrinos and antineutrinos aren’t Dirac fermions but are actually Majorana particles, then an atomic nucleus that was unstable against double beta decay could actually exhibit two different types of double beta decay.

On the one hand, there would be double-neutrino double-beta decay, where the parent nucleus would emit two electrons and two neutrinos, transforming two of the neutrons in the nucleus into protons in the process.

But on the other hand, there would also be neutrinoless double-beta decay, where the parent nucleus emits a neutrino, and that neutrino then gets absorbed as an antineutrino, leading to the emission of two electrons and the conversion of two neutrons in the nucleus into two protons, with no leftover energy or momentum carried away, as there’s no outgoing neutrino (or antineutrino signature).

When a nucleus experiences a double neutron decay, two electrons and two neutrinos get emitted conventionally. If neutrinos obey the see-saw mechanism and are Majorana particles, neutrinoless double beta decay should be possible. Experiments are actively looking for this, but so far have only discovered two-neutrino double beta decay, which describes the decay pathway of the longest-lived unstable isotopes known.

If neutrinos are Majorana in nature, they would be the first particles with such properties ever discovered. It would potentially indicate a much richer neutrino signature than what is presently known. Some possibilities for what else a neutrino could do would be as follows.

• If neutrinos are Majorana, they could imply the existence of sterile neutrinos, which could lead (through the see-saw mechanism) to them potentially being a type of ultra-heavy dark matter.
• If neutrinos are Majorana, then it’s easy to concoct a scenario in the early Universe where a lepton asymmetry (difference between the number of leptons minus the number of antileptons) is easy to create, which would then lead to a baryon asymmetry through a first-order electroweak phase transition in the later Universe.
• And there’s also a possible connection between dark energy and neutrinos. If you ask “how strong is dark energy?” and you put in the one dimensionless energy scale we have from combining fundamental constants the Planck scale you get the worst prediction in all of physics, where your calculated expectation is 120 orders of magnitude too high. But if you replace that with an energy scale of about 0.003 electron-volts, which just might be the neutrino mass scale, you get a prediction that matches observations.

These are three of the biggest unsolved problems in modern physics and astrophysics today: the dark matter problem, the matter-antimatter asymmetry problem, and the dark energy problem. Neutrinos, if nature is kind and we continue to investigate it, might hold the solution not just to one of them, but potentially to all three.

This to-scale diagram shows the relative masses of the quarks and leptons, with neutrinos being the lightest particles and the top quark being the heaviest. No explanation, within the Standard Model alone, can account for these mass values. We now know that neutrinos can be no more massive than 0.45 eV/c² apiece, meaning that the difference between a neutrino’s mass and an electron’s mass is more than three times as large as the difference between the electron’s mass and the top quark’s mass.

There’s tremendous excitement within the physics community about three classes of experiment that are continuing to investigate the nature of the elusive neutrino.

• There are direct tritium beta decay experiments (like KATRIN) that are ongoing, seeking to measure the individual neutrino mass eigenstates (ν₁, ν₂, and ν₃) directly.
• There are neutrinoless double beta decay experiments (like GERDA and MAJORANA) underway, which have set upper limits on the rate at which that process can occur at, while measuring double neutrino double beta decay events to the greatest precisions ever.
• And there are neutrino oscillation experiments that are planned to occur with greater precision, larger and more sensitive detectors, and multiple baseline distances than ever before, including Hyper Kamiokande in Japan, the Deep Underground Neutrino Experiment in the USA (which may be in extreme jeopardy, as the US Department of Energy, which oversees particle physics in the United States, just completely eliminated its High Energy Physics Advisory Panel), and the Jiangmen Underground Neutrino Observatory in China.

There have been all sorts of efforts to advance physics beyond the Standard Model. From astrophysics, we have all sorts of evidence that the Standard Model isn’t enough on its own; it can’t explain the matter-antimatter asymmetry, dark matter, or dark energy on its own. But neutrinos already stand in defiance of the original Standard Model: they have tiny but non-zero masses, and are the one known particle that could have a shot at solving any or all of these existential cosmic puzzles. After all, there are still around 10⁹⁰ of them left over from the Big Bang within merely our observable Universe. A full 95 years after first being formulated, the elusive neutrino remains the most mysterious known particle in the entire Universe.